In the Value section, we learned that a value in Elm is anything that can be produced as a result of a computation. We also learned that Elm values are immutable, which means once created, we can never change them. Once again, Elm has borrowed this concept of immutability from mathematics. For example, the number 3 in mathematics is a value that cannot be changed. Sure, we can add or subtract other numbers from it, but 3 itself will never change. If we add 1 to 3, we get 4 — a completely new number. This is exactly what happens when we try to modify a value, such as a list, in Elm.
Immutable Constants
All constants in Elm are immutable. Once assigned, a constant cannot be reassigned a different value in the same scope. If you are coming to Elm from an imperative language this might sound confusing. In those languages, it’s common to write code like this:
var x = 1;
x = x + 1;It means assign x as a name to an expression that evaluates to 1. Then take the current value of x, add 1 to it and assign the result back to x essentially mutating its original value. Let’s try that same code in Elm to see what happens.
> x = 1
1
> x = x + 1
-------------------------- CYCLIC DEFINITION ----------------------------
The `x` value is defined directly in terms of itself, causing an infinite loop.
3| x = x + 1
^
Are you trying to mutate a variable? Elm does not have mutation, so when I
see x defined in terms of x, I treat it as a recursive definition. Try giving
the new value a new name!
Maybe you DO want a recursive value? To define x we need to know what x is, so
let’s expand it. Wait, but now we need to know what x is, so let’s expand it...
This will keep going infinitely!As usual, Elm provides a descriptive error message pointing out that it doesn’t allow mutation. Definitions like x = x + 1 are not allowed in both algebra and Elm because we already defined x as 1 and now we are saying that x is 2. It can’t be both at the same time.
If you pay close attention to the error message, Elm is actually trying to tell us why it can’t allow mutation in this case. When we try to evaluate an expression such as x = x + 1, we’re asking Elm to create a constant named x that is defined in terms of itself. So Elm will try to expand the definition further as shown below creating an infinite loop:
- Recursive Definition
x = x + 1x = (x + 1) + 1x = ((x + 1) + 1) + 1x = (((x + 1) + 1) + 1) + 1x = ((((x + 1) + 1) + 1) + 1) + 1...
Elm also tells us that we can fix this by giving the x + 1 expression a new name like this:
> x = 1
1
> xPlusOne = x + 1
2In an imperative language, x is appropriately called a variable because its value can vary even after its creation. Whereas in Elm, x is a constant. Because Elm doesn’t allow mutation, the language has no variables. Does this mean we can’t use the same name to represent other values anywhere else in our code? Not really. Once assigned, a constant cannot be reassigned to a different value only in the same scope.
Constants like x are local to their scope so their life is usually short. When their scope is no longer alive, they will be discarded. After that we can reuse the name to represent other values. The function definition shown below is a good example of a constant in a limited scope. Go ahead and add it right above main in Playground.elm.
multiplyByFive number =
let
multiplier =
5
in
number * multiplierNow call multiplyByFive from main.
main =
multiplyByFive 3
|> Debug.toString
|> Html.textRun elm reactor from the beginning-elm directory in terminal if it’s not running already and go to http://localhost:8000/src/Playground.elm in a browser. You should see 15.
We learned in chapter 3 that let expression is one of the ways we can create a local scope in Elm. The multiplier constant in multiplyByFive function above is bound to 5. As soon as the program execution steps out of the let expression, multiplier won’t be alive anymore. If we try to reassign a different value to it inside the let expression Elm will complain. Replace the multiplyByFive function definition in Playground.elm with the following code.
multiplyByFive number =
let
multiplier =
5
multiplier =
6
in
number * multiplierRefresh the page at http://localhost:8000/src/Playground.elm and you should see the following error.
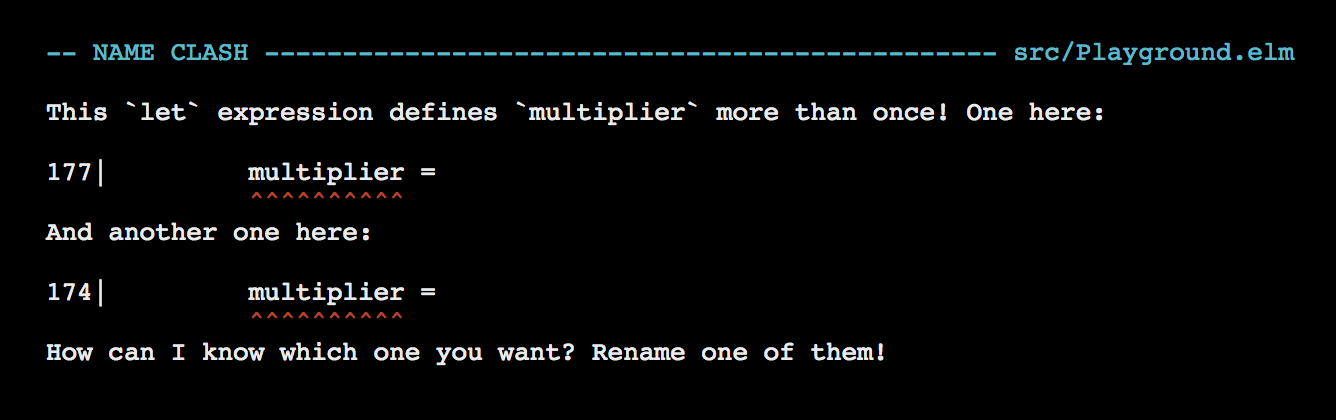
Let’s move the second definition of multiplier out of the multiplyByFive function and see what happens.
multiplier =
6
multiplyByFive number =
let
multiplier =
5
in
number * multiplierRefresh the page at http://localhost:8000/src/Playground.elm once again and you should see a different error.
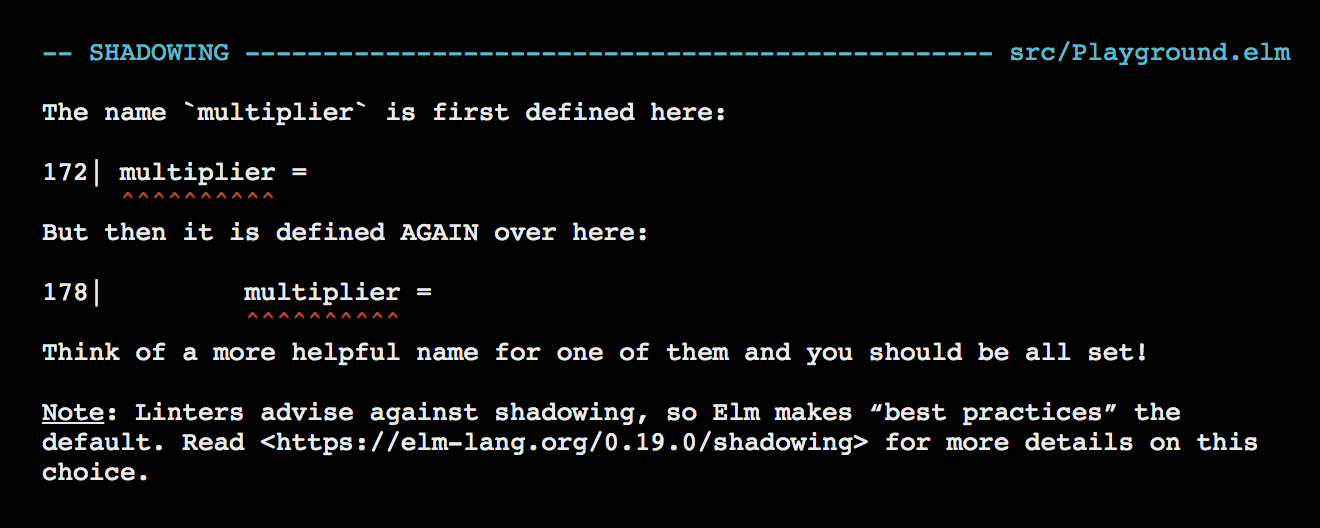
- Shadowing
- Shadowing occurs when a constant defined within a certain scope has the same name as a constant defined in a outer scope. It often makes code hard to read and may create unnecessary bugs. Most programming languages allow shadowing by default, but Elm doesn’t. It’s not surprising because two things Elm cares a lot about are minimizing bugs and easy-to-read code. You can read more about shadowing here.
Let’s rename the multiplier constant in outer scope to outerMultiplier.
outerMultiplier =
6
multiplyByFive number =
...Now, if you refresh the page at http://localhost:8000/src/Playground.elm once more, the error should be gone and you should see 15 again. Next, let’s try the same thing in elm repl.
> multiplier = 5
5
> multiplier = 6
6Hmm… why does the repl allow us to reassign a different value to multiplier? That’s because the repl works a little differently. Whenever we assign a different value to an existing constant, the repl rebinds the constant to a new value. The rebinding process kills the constant and brings it back to life as if the constant was never pointing to any other value before. Without this rebinding process, it would be difficult to try things out in the repl.
Immutable Collections
In the Modifying Tuples section, when we were trying to understand why we couldn’t modify tuples, we discovered that all collections in Elm are also immutable. Because it’s hard to build anything useful if we can’t transform data from one form to another, Elm uses a clever technique to give us the appearance of adding or removing values from a collection.
> numbers = [ 1, 2, 3 ]
[1,2,3]
> 0 :: numbers
[0, 1, 2, 3]
> List.drop 1 numbers
[2,3]In the example above, we used the :: operator to add 0 to the beginning of the numbers list and used the drop function to remove the first element from the same list. Although we were able to add and drop values from the list, its original content has remained intact.
> numbers
[1,2,3]Elm created a copy of the original list, added 0 to it, and returned it as the result. While this was all happening, the original list remained unchanged.
Quote: “In a purely functional program, the value of a [constant] never changes, and yet, it changes all the time! A paradox!” - Joel Spolsky
Performance Implications of Immutability
Creating a new copy of data whenever we update it sounds like an expensive operation from performance standpoint. This is a valid concern. However, Elm is smart and it knows the existing data is immutable. So it reuses it, in part or as a whole, when building new data. Consequently, immutability doesn’t really incur any performance penalty in Elm. Here is how the internal representation of the new list from the example above looks:
Benefits of Immutability
We have talked a lot about how constants and values are immutable in Elm, but what benefits do we get from it? The primary benefit of immutability is that it allows us to write programs that behave as expected. This leads to highly maintainable code. To make this more concrete, let’s compare an implementation in Elm with another language that doesn’t have immutability baked in. JavaScript fits the bill.
Back in the Sorting a List section, we learned how to sort a list containing the top seven highest scores (shown below) from regular season games in NBA history in different orders.
[ 316, 320, 312, 370, 337, 318, 314 ]Let’s say the NBA has decided to allow a new performance-enhancing drug that has the potential to double each player’s scoring. This will make it hard to compare current players against players who have already retired, so we need to adjust all historical stats. Let’s write a function to do that. We will first write it in JavaScript — a language that allows mutation — to find out what could go wrong.
Note: Don’t worry if you have never used JavaScript before. The example below is quite simple and you should be able to follow along without any difficulty.
Create a new file called experiment.js in the beginning-elm directory and add the code below to it.

var scoreMultiplier = 2;
var highestScores = [316, 320, 312, 370, 337, 318, 314];
function doubleScores(scores) {
for (var i = 0; i < scores.length; i++) {
scores[i] = scores[i] * scoreMultiplier;
}
return scores;
}-
highestScores— A variable that points to a list of highest scores. -
scoreMultiplier— A variable that points to a number used to multiply each element in thehighestScoreslist. -
doubleScores— A function that takes a list of scores; iterates through each element in the list using aforloop; and multiplies them by a value held in thescoreMultipliervariable.
Next, load experiment.js in index.html, which is also located inside the beginning-elm directory.
<!DOCTYPE html>
<html>
.
.
<body>
.
.
<script src="elm.js"></script>
<script src="experiment.js"></script>
.
.
</body>
</html>Note: As mentioned in the Elm Compiler section, it’s perfectly fine to use both Elm and JavaScript code side by side.
Open index.html in a browser and then go to the browser console.
- Opening browser console
- Instructions for opening the browser console depends on which browser you’re using. Please read this nice tutorial from WickedlySmart to learn how to open the console on various browsers.
Verify that the code in experiment.js is loaded successfully by printing the following values from the console.
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> scoreMultiplier
2Let’s see doubleScores function in action. Call it from the console like this:
> doubleScores(highestScores)
[632, 640, 624, 740, 674, 636, 628]So far everything looks good. Now let’s go ahead and redefine the scoreMultiplier variable in experiment.js so that it points to 3 instead.
var scoreMultiplier = 2;
var highestScores = [316, 320, 312, 370, 337, 318, 314];
var scoreMultiplier = 3;
.
.Notice the original definition var scoreMultiplier = 2; is still there. Reload index.html in the browser so our changes to experiment.js will take effect. After that, apply the doubleScores function to the highestScores list by typing the code below into the browser console.
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> doubleScores(highestScores)
[948, 960, 936, 1110, 1011, 954, 942]doubleScores now triples each element in the highestScores list. This is problematic. The new behavior does not match its name. We want it to double the scores no matter what, so that other people reading our code aren’t confused by the mismatch.
Unfortunately, most languages that allow mutation suffer from this problem. It’s especially frustrating when the redefinition happens in a remote part of the code, which is hard to detect. At least in the example above, we can see that scoreMultiplier is being redefined close to the original definition and we can correct it. But in the real world, most problems caused by mutation tend to manifest after the code has been deployed to a production environment.
How does Elm deal with this situation? Well, let’s reimplement the code above in Elm to find out. Add the following code right above main in Playground.elm.
scoreMultiplier =
2
highestScores =
[ 316, 320, 312, 370, 337, 318, 314 ]
scoreMultiplier =
3
doubleScores scores =
List.map (\x -> x * scoreMultiplier) scoresRefresh the page at http://localhost:8000/src/Playground.elm and you should see the following error.

It’s exactly the same error we got in the Immutable Constants section above. Elm doesn’t allow us to redefine scoreMultiplier in the same scope. Remove the second definition of scoreMultiplier from Playground.elm.
scoreMultiplier =
3Mutation
The JavaScript code above has one more issue: it mutates the original highestScores list. Reload index.html in browser and enter the following code in console.
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> doubleScores(highestScores)
[948, 960, 936, 1110, 1011, 954, 942]
> highestScores
[948, 960, 936, 1110, 1011, 954, 942]As you can see the values inside the highestScores list have changed. This is also problematic. To understand why, let’s remove the redefinition var scoreMultiplier = 3 from experiment.js and add two new functions below the doubleScores function like this:
var scoreMultiplier = 2;
var highestScores = [316, 320, 312, 370, 337, 318, 314];
function doubleScores(scores) {
for (var i = 0; i < scores.length; i++) {
scores[i] = scores[i] * scoreMultiplier;
}
return scores;
}
function scoresLessThan320(scores) {
return scores.filter(isLessThan320);
}
function isLessThan320(score) {
return score < 320;
}As its name suggests, the scoresLessThan320 function returns all scores that are less than 320. It delegates the task of checking whether a score is less than 320 or not to the isLessThan320 function. Reload index.html in browser and call the scoresLessThan320 function from console like this:
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> scoresLessThan320(highestScores)
[316, 312, 318, 314]scoresLessThan320 gives us what we expect. But what will happen if we apply the doubleScores function before scoresLessThan320? To find out let’s reload index.html in browser one more time so that we’re starting fresh. After that, apply the functions as shown below in console.
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> doubleScores(highestScores)
[632, 640, 624, 740, 674, 636, 628]
> scoresLessThan320(highestScores)
[]scoresLessThan320 reports that there are no scores below 320, which is incorrect. This is because doubleScores doubled the values and saved them back into the original list which we ended up passing to scoresLessThan320 without realizing that it has already been changed.
What we really intended to happen was this:
How to Avoid Mutation?
Can this problem be avoided in JavaScript? Absolutely. Replace the current implementation of doubleScores in experiment.js with this:
function doubleScores(scores) {
var newScores = [];
for (var i = 0; i < scores.length; i++) {
newScores[i] = scores[i] * scoreMultiplier;
}
return newScores;
}doubleScores doesn’t modify the existing list anymore. Instead it always returns a new one. Refresh the browser and call doubleScores and scoresLessThan320 in the same order as before.
> highestScores
[316, 320, 312, 370, 337, 318, 314]
> doubleScores(highestScores)
[632, 640, 624, 740, 674, 636, 628]
> scoresLessThan320(highestScores)
[316, 312, 318, 314]Now it works as expected. Let’s try this in Elm to see if we will get different results depending on which order we call the scoresLessThan320 function. Add the following definitions right above main in Playground.elm
scoresLessThan320 scores =
List.filter isLessThan320 scores
isLessThan320 score =
score < 320To properly compare the results from JavaScript and Elm, we need to load the code from Playground.elm into elm repl. Before we do that though, we need to expose some values from the Playground module. Modify the first line in Playground.elm to this:
module Playground exposing
( doubleScores
, highestScores
, main
, scoresLessThan320
)Note: We’ll discuss the syntax for exposing valus from a module in detail later in the Creating a Module section.
Now we’re ready to import the Playground module in elm repl.
> import Playground exposing (doubleScores, highestScores, scoresLessThan320)We exposed doubleScores, highestScores, and scoresLessThan320 so that we don’t have to prefix the module name when we use them. Not having prefix makes it easier to compare our Elm code with the JavaScript code listed above. As mentioned in the Strings section, be careful not to run into name collision when exposing values like this.
One other thing we need to keep in mind is that the Playground.elm file must be located inside the src directory. Otherwise, elm repl won’t know about it because in the elm.json file we have specified src as the only source directory.
{
.
.
"source-directories": [
"src"
],
.
.
}Let’s say we decided to move Playground.elm to a new directory called code. Now we’ll have to include code in source-directories as shown below, otherwise the repl won’t find it.
{
.
.
"source-directories": [
"src",
"code"
],
.
.
}Now let’s apply scoresLessThan320 before doubleScores and see what we get.
> highestScores
[316,320,312,370,337,318,314]
> scoresLessThan320 highestScores
[316,312,318,314]
> doubleScores highestScores
[632,640,624,740,674,636,628]We get what we expect. Now let’s apply scoresLessThan320 after doubleScores.
> highestScores
[316,320,312,370,337,318,314]
> doubleScores highestScores
[632,640,624,740,674,636,628]
> scoresLessThan320 highestScores
[316,312,318,314]Again, we get what we expect. No matter which order we apply the functions in, we get the exact same result. In Elm, we don’t need to implement scoresLessThan320 in a special way for it to behave consistently.
Although we were able to resolve the issue introduced by mutation in JavaScript by explicitly returning a new list, we had to be cognizant of the fact that immutability isn’t baked into JavaScript. That made us take extra precaution. This can get tiresome as the code base grows. However, in Elm List.map (and all other functions in the List module) always return a new list by default. Having immutability baked into the language itself allows us to completely avoid problems like these.


